Qualche anno fa un gruppo di fisici di Bologna iniziò a studiare un modello di mobilità urbana dal nome “Mobilis in Mobile”, implementato al computer con lo scopo di fare della statistica, di
creare uno strumento didattico, ma soprattutto per iniziare a fare attività di laboratorio al computer, cioè in un ambiente virtuale dove la realtà potesse essere codificata e controllata da
semplici istruzioni in linguaggio C++ per andare alla ricerca di fenomeni e grandezze relativi al caso in studio.
Oggi presentiamo un simulatore più maturo, che gode di un approccio teorico multidisciplinare e condiviso sotto il profilo scientifico, urbanistico e sociologico. Tant’è che dopo un test sulla
città di Rimini che ha dato la speranza d’ulteriori approfondimenti ed applicazioni, si è arrivati al primo confronto con dati di mobilità reali grazie alla collaborazione con il Dipartimento di
Sociologia dell’Università Milano Bicocca. Un vero e proprio “esperimento fisico” in cui si sono confrontati “percorsi statistici”, dati dal modello cronotopico implementato nel Mobilis, con i
tracciati registrati.
Dopo aver eseguito diversi test di calibrazione del modello con valori arbitrari, si è reso necessario effettuare una calibrazione, anche in un caso relativamente semplice, come quello di Milano
Bicocca, con valori dei parametri e dell’input dati dall’indagine sul campo. Attraverso un confronto tra flussi simulati e reali verificando una loro eventuale congruenza o discordanza si riscontra
se le ipotesi usate nell’implementazione del modello sono buone o bisogna rigettarle. Nel caso del campus Universitario di Milano Bicocca si è trovato che i flussi reali registrati e quelli
simulati sono in buon accordo convalidando che le ipotesi di mobilità su cui si basa il modello Mobilis sono buone.
Introduzione
Prima di descrivere gli ingredienti del modello cronotopico è necessario soffermarsi sulla definizione di città e mobilità intese, nell’ambito disciplinare delle scienze
urbanistiche e fisiche, come paradigmi di sistema complesso [1].
I modelli globali e riduzionisti si sono dimostrati inadatti a descrivere la dinamica urbana. La sua natura complessa porta all'emergere di proprietà
inaspettate, d’autorganizzazione [2], alla frontiera tra ordine e caos. Questa complessità è generata dall'interazione non deterministica tra i
cittadini, dotati di libero arbitrio, e la topologia urbana, metropolitana.
La governance delle metropoli è uno dei problemi principali oggi esistenti [13], data la sua stretta correlazione con la qualità della vita in
tutti i suoi aspetti, dalla sicurezza alla bellezza alla salute. La mobilità assume particolare rilievo in quanto non si può parlare di libertà dell’uomo senza definire la sua libertà di
movimento.
Non è possibile modellare la mobilità senza usare un insieme di concetti e conoscenze veicolati dall’urbanistica, dalla psicologia, dall’architettura, dall’ingegneria dei trasporti, dalla
geografia, dall’economia, eccetera.
Il gruppo di Fisica della Città dell’Università di Bologna, studiate a fondo le implicazioni del modello cronotopico, ha creato un software di dinamica
mesoscopica, i cui componenti elementari sono i cittadini dotati di propensioni e comportamenti “intelligenti” (Intelligenza Artificiale). Nel modello il cittadino può scegliere diversi mezzi
di trasporto. L’interazione con la topologia urbana è modellata introducendo i cronotopi ossia gli agenti primigeni della dinamica temporale urbana
[3]; in altre parole, sono aree urbane dove sono insediate attività calendarizzate (es. Università, Ospedale, ufficio postale eccetera) che
diventano attrattori per i cittadini secondo le propensioni messe in agenda dall'individuo (gli studenti, ad esempio, avranno una certa propensione ad andare all'Università in certe ore della
giornata). Il modello, una volta implementato, diventa un vero e proprio laboratorio virtuale (mondo virtuale) dove è possibile osservare, sperimentare e studiare la dinamica per scoprire eventuali
“leggi” proprie del sistema complesso “mobilità urbana”.
Tuttavia non secondario rispetto alla modellizzazione virtuale è il problema della sperimentazione, avente lo scopo di verificare la corrispondenza tra il modello e la realtà. Questo è un problema
delicato e difficile da affrontare in quanto non esiste una teoria generale della misura fisica per fenomeni complessi come invece esiste per la fisica newtoniana e quantistica, ed anche per
fenomeni spiegati all'interno della teoria della relatività. La stessa definizione di complessità [5], in letteratura, cambia da autore ad autore,
si possono vedere per esempio le definizioni che danno Stuart Kauffman [6], Giorgio Parisi [7],
Bruno Giorgini e Giorgio Turchetti [8]. Per quanto riguarda i sistemi complessi se l'osservatore non è parte del sistema, non è chiaro fino a che
punto arrivi la sua conoscenza del funzionamento interno al sistema. Se l’osservatore è parte del sistema, l'autoosservazione porta ad un regresso all'infinito che rende impossibile la conoscenza
completa del sistema stesso [9].
La mobilità dei cittadini, fenomeno complesso, a sua volta avviene all'interno di un sistema esso stesso complesso quale la città.
Usando le parole di C. Levi Strauss possiamo descrivere tale complessità.
Agglomerato di esseri che racchiudono la loro storia biologica entro i suoi limiti e la modellano con tutte le loro intenzioni di creature pensanti (...) la città risulta contemporaneamente della procreazione biologica, dell'evoluzione organica e della creazione estetica. Essa è, nello stesso tempo, oggetto di natura e soggetto di cultura.
Tuttavia questa descrizione chiara e semplice definisce solo l'aspetto qualitativo della complessità, altro è passare ad una sua descrizione quantitativa, per via fisico matematica, usando il linguaggio proprio delle cosiddette “scienze esatte” [10]. In questa sede vogliamo descrivere i primi passi fatti in tale direzione attraverso alcuni “esperimenti virtuali” e “reali” portati avanti nell’ambito di quella che abbiamo definito la Fisica della Città.
Storicamente i modelli fisico-matematici globali si sono rilevati inadeguati a descrivere l'evoluzione della città [11]. Non a caso
uno studio ed una modellazione dinamica furono proposti già da M. Batty nel 1971 [12]. È tuttavia difficile riuscire a costruire un
modello di mobilità in grado di descrivere la dinamica puntuale del sistema stesso [13]. Da una parte la mobilità è espressione della società,
si sviluppa in essa, dall’altra definisce l’evoluzione della società in una certa direzione anziché un’altra [14]. Non a caso i grandi progetti
infrastrutturali per la pianificazione della mobilità si sviluppano in decenni, nei quali la società si evolve e al tempo stesso condizionano lo sviluppo dell’economia dell’area sulla quale si
realizzano.
Batty pone l'accento sulle principali difficoltà che s’incontrano trattando fenomeni complessi come la mobilità e la città. Da una parte le equazioni che descrivono tali sistemi sono
intrinsecamente non lineari e quindi, non hanno in genere, soluzioni analitiche [15]. Dall'altra sono difficilmente acquisibili delle serie
temporali di dati sufficientemente lunghe, ossia quanti dati dobbiamo registrare, affinché li possiamo considerare “sufficienti”, per produrre una descrizione abbastanza ragionevole del fenomeno in
esame [16]. Per quanto riguarda la non linearità delle equazioni dinamiche lo sviluppo della potenza di calcolo, della computer science, ha
permesso di ridurre di molto la portata di tale difficoltà attraverso un proliferare di modelli fisico matematici, implementati su calcolatore e in grado di generare mondi ed esperimenti virtuali
complessi [17]. Ma nel ventre della modellizzazione virtuale è racchiuso il grosso rischio che il “principio di simulazione” abbia ragione del
“principio di realtà” [18]. Più cresce la complessità dei modelli e delle simulazioni [19], tanto più è importante il confronto col fenomeno reale. Tale confronto serve per verificare la congruenza tra la realtà e la sua descrizione implementata nel modello e tra la
realtà osservata e quella virtuale prevista dal modello [20]. Per quanto riguarda la seconda difficoltà indicata da Batty non è ancora risolta
in modo soddisfacente, sia sul piano della raccolta di dati già esistenti sia sul piano della messa in opera di esperimenti abbastanza controllabili, perché si ha a che fare con un insieme molto
ampio di osservabili e di componenti elementari e non esiste una teoria generale che ci guidi per la scelta delle osservabili e dei campioni
statistici sufficienti ad una descrizione.
In quest’articolo esporremo dapprima lo stato dell’arte dei modelli usati per descrivere la mobilità (in particolare quella zigzagante [21]), successivamente, dopo aver descritto le potenzialità e le caratteristiche del modello, passeremo ad una calibrazione di Mobilis attraverso i dati statistici delle popolazioni presenti, le frequenze degli autobus, la calendarizzazione delle attività cronotopiche presenti. Descriveremo, infine, la procedura usata per rilevare i dati, per farne l’analisi e per confrontarli con i flussi simulati dal modello opportunamente calibrato.
Lo stato dell'arte dei modelli di mobilità
Già negli anni ’60 si assiste ad un proliferare di modelli matematici e fisici utili. Tali modelli prevalentemente globali e riduzionisti subisco una drastica trasformazione negli anni ’70 quando
M. Batty sottolinea la necessità di trattare la città da un punto di vista dinamico. Egli tuttavia si sofferma sullo studio della dinamica di crescita della città [22] senza prendere in considerazione la dinamica della sua popolazione.
Nel corso degli anni si sviluppano un'ampia collezione di modelli [23], in special modo di tipo origine destinazione [24], assieme ad una massiccia raccolta di dati, soprattutto per quanto riguarda il traffico autoveicolare [25],
trattato sia in modo stocastico che deterministico, attraverso equazioni simili a quelli delle reti idrauliche (fluidodinamica).
Mobilità origine-destinazione e mobilità zigzagante
Definiamo la mobilità come la propensione di un cittadino a muoversi in una topologia spazio-temporale che, nel nostro caso, corrisponde ad una generica planimetria urbana, dove si insediano funzioni sparse o raggruppate in macroaree e fruibile da varie tipologie di cittadini. La mobilità, quindi, è una proprietà del singolo che la esercita con diversi mezzi: a piedi, sulle due ruote, tramite trasporto pubblico e autoveicoli privati, eccetera. La possiamo definire sostenibile non solo quando l'impatto ambientale ed economico è basso, ma, soprattutto, quando questi diversi mezzi concorrono, cooperano ad una mobilità fluida, comoda e bella.Tradizionalmente la mobilità è partita in due sottoclassi, quella origine destinazione (O-D) e quella zigzagante o asistematica.
Per mobilità O-D si intende quella in cui l'origine e la destinazione sono ben definite, nello spazio e nel tempo e corrispondono quasi sempre al percorso casa-lavoro. Nella società tayloristica, caratterizzata dai grandi agglomerati, bacini d’attrazione della maggior parte dei lavoratori, la mobilità dominante era quella O-D. Questo tipo di mobilità è abbastanza regolare e quasi periodica ed è perciò prevedibile, almeno in linea di principio. La mobilità asistematica, mentre, non presenta regolarità spazio-temporali ed è molto più difficile modellarla attraverso matrici O-D, perché la quantità d'informazione richiesta per scrivere queste matrici è enorme. Possiamo affermare che la mobilità asistematica è caratterizzata da un alto tasso d’incertezza e imprevedibilità intrinseche. Finché la mobilità asistematica è una piccola percentuale di tutta la mobilità, la si può trascurare. Ma quando diventa dell'ordine del 50% una buona modellizzazione della mobilità non può non considerarla. Per esempio se consideriamo l'intera regione Emilia-Romagna, vediamo che il 53% degli spostamenti extracomunali sono di tipo sistematico e ad orario vincolato, mentre ben il 47% sono asistematici e ad orario libero [26]. Questo dato si accentua negli spostamenti urbani.
Bisogna, inoltre, aggiungere che la popolazione in movimento non è univocamente definibile, ma, piuttosto, è un insieme di diverse categorie sociali. Ci sono i residenti (e perciò censibili) a cui si aggiungono popolazioni fluttuanti che arrivano in città, con gli statuti più diversi, per le occasioni più diverse, e restano per i periodi più diversi, chi viene per fiere o mostre o altri eventi culturali, economici, politici, artistici, spettacolari, chi per un tempo di lavoro, chi per un tempo di studio, chi per un tempo di vacanza, chi per un fine settimana, chi per un mese, eccetera, senza dimenticare i molti, e destinati a crescere, migranti senza lavoro fisso, e spesso senza dimora fissa. Insomma abbiamo tutta una popolazione di girovaghi su grande e piccola scala - in linguaggio sociologico city users [27] - che zigzaga nella città e nell'area metropolitana, rendendo la mobilità assai più complessa di quanto non fosse fino a pochi anni fa.
I modelli urbani
Il problema di costruire modelli utili per studiare le dinamiche della crescita urbana, le trasformazioni sociali e la mobilità dei cittadini, fu posto a partire dagli anni ’60. Questi modelli furono sviluppati sia per tentare di spiegare la struttura complessiva della città, intesa come oggetto intrinsecamente razionale (quindi matematizzabile, almeno per via analogica), sia per aiutare a predire le conseguenze della pianificazione urbana (planning), considerata allora come globale, centralizzata e sottesa da una filosofia “illuministica” (nei casi migliori). In breve, furono costruiti modelli globali, macroscopici, statici e/o stazionari con differenti approcci. Quelli meccanici (modelli gravitazionali), quelli termodinamici (modelli entropici) o, specialmente negli USA e nel mondo anglosassone, modelli basati sulla teoria dei giochi, o su equazioni del tipo Lotka-Volterra, in specie per descrivere i processi decisionali (con i relativi conflitti) di pianificazione. Scendendo nello specifico dei modelli O-D, sono definiti due punti, l'origine e la destinazione, e un solo percorso nel caso deterministico, o più percorsi (archi) con una probabilità assegnata a priori, nel caso stocastico. Le due variabili fondamentali sono la capacità delle strade e il volume dei veicoli pubblici e privati, e il parametro critico è il rapporto tra loro. Di solito i valori delle variabili sono scelti a tempi costanti e mediati su un certo numero di questi intervalli temporali per ottenere un comportamento medio. Questi modelli, quindi, descrivono una situazione d’equilibrio macroscopico, mentre le proprietà dinamiche del singolo sono trascurate. Danno risultati affidabili soltanto se il traffico è sufficientemente regolare e non affetto da forti, improvvisi e inaspettati cambiamenti di flusso. I modelli O-D non si possono usare per studiare possibili regimi turbolenti ed eventuali transizioni di fase, non sono in grado di descrivere la mobilità zigzagante [28].Come si è detto il panorama è cambiato agli inizi degli anni ’70 perché i modelli su larga scala sono troppo lontani dalla realtà [29] e perché si comincia a studiare la città come sistema dinamico [30]. Nello stesso periodo assistiamo allo sviluppo di studi attinenti i sistemi non lineari e complessi deterministici e stocastici. Sviluppo che è andato di pari passo con la crescita esponenziale della potenza computazionale delle macchine e l'invenzione di nuovi linguaggi a oggetti (object oriented) che aprono la possibilità di esperimentare sistemi complessi, usando il calcolatore come laboratorio virtuale. Inoltre nell'ambito urbanistico cambia il concetto di planning. Gli urbanisti hanno scoperto come le azioni del singolo, così come le opinioni e le iniziative di libere, e spesso spontanee, associazioni di cittadini, possano essere rilevanti ai fini della pianificazione territoriale, dalla strada al quartiere, alla città intera. La percezione dello spazio-tempo urbano cambia dal singolo fino ai differenti gruppi sociali, di interesse, culturali eccetera. Da qui il piano regolatore viene concepito come strumento in grado di armonizzare queste diversità e non come modo di governo centralizzato e precostituito dall'alto. La pianificazione diventa in questo modo un processo sensibile alle rapide variazioni degli atteggiamenti individuali e ai comportamenti collettivi. Nel linguaggio della fisica si può dire così: non esiste più un osservatore generale privilegiato ma una miriade di osservatori locali, per così dire egualitari, ciascuno con i propri strumenti di misura. Soltanto la loro composizione può dar luogo ad una visione comune. Composizione che sarà sempre costituente, ossia dinamica, e mai costituita, cioè mai statica.
Il modello Mileto/Manhattan: Mobilis
Scopo ultimo del modello è quello di riprodurre la mobilità integrata all’interno delle città, sia quella sistematica che quella asistematica. Per coglierne la varietà e la mutevolezza, la modellizziamo come fenomeno emergente di tutte le sottodinamiche legate all’entità mobile rappresentata dal cittadino che applica la propria strategia di mobilità attraverso la scelta tra tutte le modalità disponibili in ambito urbano. Inizialmente abbiamo implementato l’interscambio tra pedone e trasporto pubblico, considerando la modalità privata (autovetture) solo sotto forma di attrito.
La mobilità descritta nel modello può essere studiata attraverso due livelli d’approssimazione:
- una mobilità individuale che mescola aspetti probabilistici e deterministici;
- una mobilità più complessa in cui il cittadino, oltre alle caratteristiche precedenti, interagisce con icronotopi
Il modello Mileto/Manhattan è definito in uno spazio discreto (network di mobilità).
In particolare, lo spazio-tempo urbano è rappresentato da un reticolo di NxN strade a cui sovrapponiamo una griglia di nxn linee di trasporto pubblico (n<N)(figura 1). Questa topologia è facilmente adattabile a qualunque planimetria urbana da quella di Rimini [31] a quella del Campus Universitario di Milano Bicocca [32]. I passi temporali sono scanditi dall'orologio del calcolatore, che definisce il normale tempo fisico, newtoniano. Su questo reticolo si muovono a caso (moto browniano) gli individui, (componenti elementari del sistema), di dimensione zero (puntiformi), saltando a ogni passo temporale da un incrocio a uno dei suoi primi vicini. L’individuo virtuale è detto mobber per distinguerlo da quello reale, in quanto è un automa intelligente in grado di processare informazioni, prendere decisioni e possedere una memoria ma non pretende di essere completamente realistico.
Il mobber inizialmente si trova nello stato di pedone (p) e si muove con velocità v (costante). Quando un mobber arriva ad un incrocio (figura 2), che può essere anche un nodo di interscambio (stazione) con le linee di trasporto pubblico, può salire su un mezzo e diventare utente (u); in presenza di più mezzi che si muovono in direzioni diverse, sceglie in modo probabilistico, oppure se in stazione non trova nessuno mezzo, il mobber attende fino al suo arrivo mettendosi in stato di attesa (a). In questo modo il mobber si può passare da uno stato dinamico all’altro (p <–>u, p <–> a, a <–> u)*.
Il tempo di simulazione e la velocità v del mobber sono sincronizzati in modo tale che un mobber-pedone impiega un tempo unitario per andare da un incrocio
all'altro. Un mobber-utente, presente su un treno, impiega un tempo unitario per percorrere la distanza tra due stazioni successive. Il rapporto tra le due velocità diventa
n/N. Ovviamente questa dinamica dei mezzi pubblici è realistica solo per le metropolitane, mentre per i mezzi di superficie (autobus, tram, filobus) entrano in gioco le possibili
perturbazioni dovute al traffico privato (rallentamenti, ingorghi, eccetera), che sono state simulate, per ora, tramite una funzione di viscosità (figura 1).
La mobilità individuale, almeno nell'approssimazione di campo medio, può essere studiata con metodi analitici. Il buon accordo trovato garantisce che l'implementazione algoritmica è esente da
patologie e/o inconsistenze interne [33].
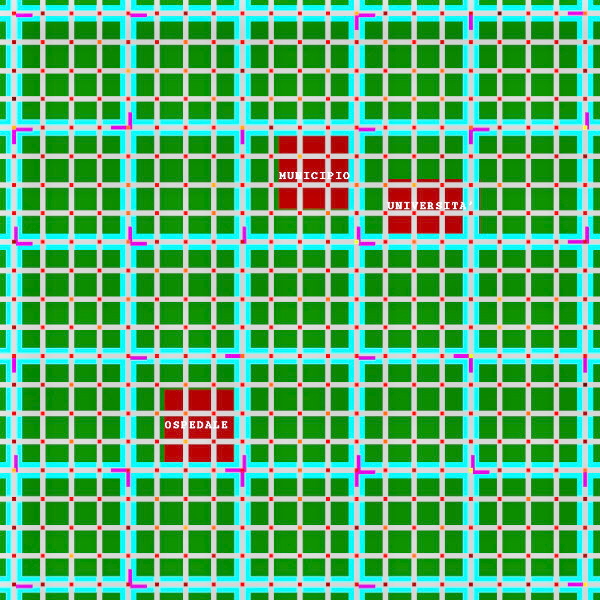
Lo stato di moto del mobber che si muove su questa planimetria può essere descritto da una successione delle 4 direzioni possibili* alto, basso, sinistra, destra che, a ogni passo
temporale, a partire dall'istante iniziale, definiscono la mossa del mobber pedone.
Il movimento del singolo sarà descritto da una stringa**. Dato il punto di partenza, quello d’arrivo si ottiene sommando vettorialmente le varie direzioni e spostando il mobber
pedone secondo il vettore somma. Ovvero tutti i movimenti possibili dopo n passi temporali sono codificati da una parola di lunghezza n, formata da 4 simboli. Si sono introdotte regole grammaticali
inibendo la presenza di simboli opposti adiacenti (*) oppure di circoli viziosi (**).
In questo modo il mobber è dotato di una sorta di memoria, che può essere a breve e/o a lungo termine. Tanto più questa memoria è estesa, tanto meno il sistema è
statisticamente puro (markoviano). Alla decisione individuale abbiamo lasciato un po’ di incertezza, un “fondo stocastico”, in modo tale che il singolo possa, in casi rari, ritornare sui propri
passi o muoversi lungo un circolo vizioso. In questo modo si salvaguarda il libero arbitrio (e l'imprevisto) anche laddove le scelte possono non apparire razionali sotto il profilo
dell'efficienza e/o dell'economia (nel nostro caso la funzione utilità è inversamente proporzionale al tempo in quanto la distanza è temporale, cioè misurata dall'orologio del calcolatore).
Al tempo fisico scandito dall'orologio del calcolatore vanno sovrapposti, almeno in linea di principio, i ritmi circadiani per fare in modo
che il mobber virtuale sia più simile ad un essere reale.
Ora possiamo descrivere la mobilità complessa che si sviluppa dall’interazione del mobber con i cronotopi, letteralmente i luoghi generatori di dinamiche temporali a
differenti scale.
Come detto in precedenza i cronotopi esercitano un’attrazione maggiore su determinate categorie di cittadini. Per esempio l'Università esercita una certa attrazione su studenti, professori,
personale tecnico e amministrativo. Questa attrazione è modellata con una forza. Non si tratta di una forza newtoniana, nel senso che non produce accelerazione, e non vale il principio d’azione e
reazione. Matematicamente l'abbiamo scritta come forza elastica. Il singolo mobber può avere una propensione per uno oppure un altro dei cronotopi presenti nell’area presa in
esame, in altre parole possiede una o più "cariche" cronotopiche che formano parte del suo corredo genetico, oltre ad alcune caratteristiche sociologiche come attività, sesso, età, eccetera. Rimane
sempre una quota di cittadini senza alcuna propensione. Per ora abbiamo distinto le propensioni in forti e deboli, per esempio è forte quella per il luogo di lavoro, debole quella
per un luogo di divertimento.
Il mobber possiede un'agenda giornaliera che indica in successione i cronotopi che intende visitare (il dato medio, che viene dagli studi sociologici, è di 2.6 obiettivi per
individuo nelle 24 ore). Nel linguaggio della dinamica abbiamo un moto stocastico con deriva. Al tempo fisico e ai ritmi circadiani si sovrappone un altro tempo che possiamo chiamare sociale,
scandito dai cronotopi, o meglio una collezione di tempi che concorrono alla formazione di questo tempo sociale. Questo tempo interagisce col tempo "sociale" dell'individuo (la sua agenda), creando
complessità, producendo l'emergenza di strutture ordinate.
Da questo punto di vista possiamo parlare di un sistema critico che si autorganizza, su base temporale. Inoltre, nel caso d’affollamento di un cronotopo tale da non permettere l'accesso,
il mobber dopo un certo tempo d'attesa, per ora uguale per tutti, va al cronotopo successivo inscritto nella sua agenda. A questo livello, salvo nel caso di un solo cronotopo che
può essere affrontato scrivendo un’equazione del tipo Fokker-Planck, non esistono soluzioni analitiche. Il laboratorio virtuale rimane il solo strumento per tentare di descrivere, comprendere, e
prevedere.
Ad ogni nodo il mobber sceglie tra diverse strade possibili usando il calcolo delle probabilità, dove la probabilità è quella di Bayes-de Finetti (figura 3) che si può definire
come la misura delle aspettative soggettive in relazione alla possibilità che si verifichi un evento.
La scelta è anche pesata da un coefficiente di qualità della strada che, allo stato attuale, nasce da tre indicatori (parametri): accessibilità, estetica, sicurezza.

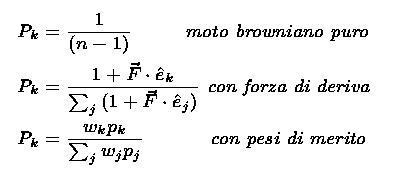
Il modello Mileto/Manhattan nei casi in cui il mobber parte da un preciso punto dello spazio-tempo e propende a un solo cronotopo forte riproduce le traiettorie dei modelli
O-D.
Il modello Mileto/Manhattan è stato oggetto di una prima applicazione nel centro storico di Rimini nel periodo invernale [34].
In questo caso, come nell’esperimento del Campus Universitario Milano Bicocca, il numero di mobber usati nelle simulazioni è dell’ordine di 10.000 unità. Si muovono su un territorio ben
delimitato, una carta cronotopica abbastanza semplice, una preponderante mobilità pedonale, una mobilità su due ruote, biciclette e motocicli oltre che quella su mezzi di trasporto pubblico.
In queste condizioni Mobilis ha riprodotto i flussi sulle strade e le densità puntuali di pedoni con discrepanze di poche decine di individui (figura 4).
L'ordine di grandezza va da alcune migliaia a dodicimila presenze durante il giorno. Questa sperimentazione virtuale ha evidenziato una fermata (stazione) d’autobus, critica per un sovraffollamento di cittadini in attesa in accordo con le osservazioni e le analisi del Comune di Rimini.
Applicazione di Mobilis all’area universitaria di Milano Bicocca
Nell'area universitaria di Milano Bicocca per la prima volta si è definito un protocollo di sperimentazione per testare le potenzialità del modello Mileto/Manhattan in un caso reale.
Nell'area di Milano Bicocca, insieme al gruppo del Dipartimento di Sociologia, in collaborazione con il Professor Guido Martinotti e il Professor Mario Boffi, integrando tra loro i diversi campi di
conoscenza e le diverse metodologie di lavoro, si è realizzato un vero e proprio protocollo di misura per la mobilità pedonale osservata nell'area al fine di verificare una possibile congruenza
quantitativa tra i flussi ottenuti dall'analisi dei dati rilevati tramite GPS e quelli prodotti dalle simulazioni.
L’area considerata è prevalentemente un Campus universitario con ritmi temporali legati al funzionamento della didattica e della ricerca. Le dimensioni sono quelle di un quartiere, più piccole di
quelle del centro storico di Rimini. La popolazione non presenta delle differenze nell'uso giornaliero dell'area. L'attività notturna è ridotta, quasi inesistente, rispetto a quella diurna.
Tuttavia le strade s'innestano sul tessuto urbano-metropolitano di Milano, sia per le fermate degli autobus urbani che per quelli dell’hinterland.
Calibrazione del modello
Il nucleo del modello Mileto/Manhatan può essere adattato ad una qualsiasi planimetria attraverso un'opportuna "calibrazione" dei dati in ingresso. Bisogna specificare, definire nella pianta
dell'area (figura 5) le attività cronotopiche (figura 8).
Per rappresentare i flussi temporali delle popolazioni presenti, con le proprie differenze sociologiche, è stata utilizzata una pianta georeferenziata per soddisfare l’esigenza di un confronto
grafico riportando sulla stessa planimetria i tracciati dei percorsi registrati tramite GPS e quelli che si ottengono dalle simulazioni.
La risoluzione della pianta permette di vedere tutti gli edifici e le strade, anche quelle prevalentemente pedonali.
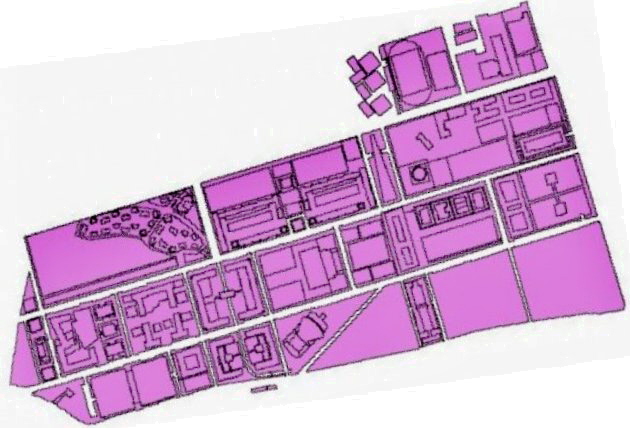
Per avere un modello realistico, tutte le strade devono essere calibrate con coefficienti d'attrattività wi, come si è detto nel paragrafo sul modello Mileto/Manhattan.
Profilo temporale e caratteristiche della popolazione
È necessario definire il profilo temporale [35].dei flussi in entrata nell'area in base all'attività lavorativa e di studio svolta da tutta la popolazione presente. Le categorie sociali, presenti nell’area, sono state suddivise in tre grandi gruppi: coloro che sono legati al mondo universitario come studenti, ricercatori e personale tecnico amministrativo; i lavoratori della Siemens e delle altre strutture private ed infine i residenti.Gli iscritti all'Università sono circa 25.000, anche se frequentano solo circa 6.000. Tra personale tecnico amministrativo e docenti sono circa 1.500. Complessivamente circa 7.500 persone gravitano intorno all'area universitaria. I dati sono riportati nella tabella 1.
| categorie sociali | % |
|---|---|
| studenti | 80 |
| professori | 14 |
| impiegati | 6 |
Tabella 1 Distribuzione delle categorie sociali presenti nell'area di Milano Bicocca
Grazie ad una ricerca sulla mobilità curata dal Professor M. Boffi, conosciamo il profilo temporale dei flussi in entrata e in uscita in funzione dell'attività svolta della popolazione universitaria. Nella figura 6 si osservi l'intervallo tra le 13:00 e le 14:00 dove la curva della popolazione in entrata nell'area (istogramma in rosso) si sovrappone con quella in uscita (istogramma in blu). Le due curve presentano i loro massimi rispettivamente il mattino tra le 8:00 e le 9:30 e il pomeriggio tra le 16:30 e le 19:00.
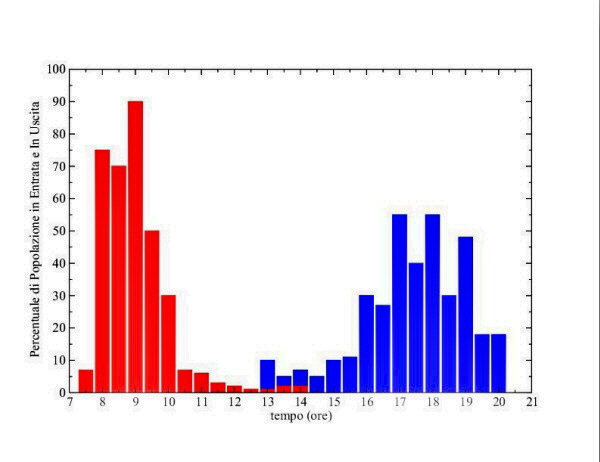
Abbiamo assunto che i 1.000 residenti escano dall'area e rientrino seguendo i ritmi temporali di cittadini che si recano a svolgere le loro attività lavorative altrove. Vista la relativa assenza d’attività serali e notturne ad eccezione del teatro degli Arcimboldi, abbiamo ragionevolmente assunto che i 1.000 lavoratori nel settore privato, visto la tipologia di competenze richieste, abbiano gli stessi orari del personale ricercatore e docente. Abbiamo costruito il file d’input che definisce il numero di pedoni presenti nell'area integrando tra loro queste informazioni (figura 7).
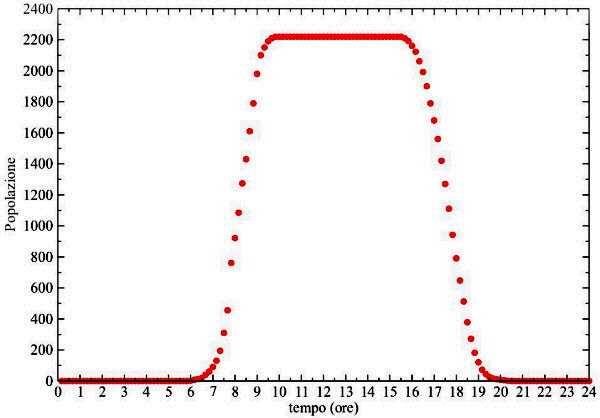
Attività cronotopiche e sorgenti
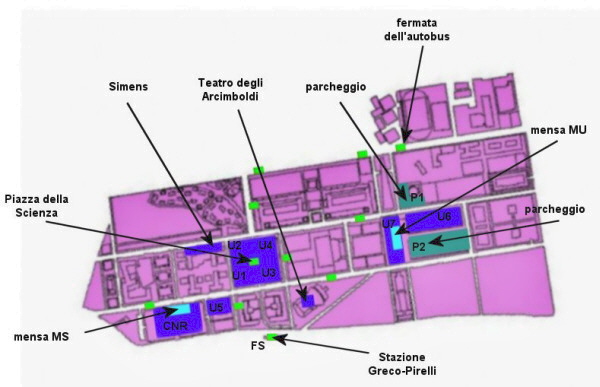
I principali cronotopi dell'area sono 6:
1. l'area prevalentemente delle facoltà umanistiche e degli uffici amministrativi che sono negli edifici U6 e U7 (con la relativa mensa MU): Sociologia, Matematica, Informatica, Scienze
Statistiche, Rettorato, Segreteria studenti, Economia, Scienze della formazione, Psicologia e Biblioteca centrale;
2. l'area delle facoltà scientifiche che sono negli edifici da U1 a U4: Scienze Ambientali, Fisica, Biblioteca scientifica, Biotecnologie e Scienze biologiche e Scienze Geologiche;
3. scienze dei materiali, edificio U5;
4. CNR e ufficio tecnico (con relativa mensa MS), edificio U9;
5. Siemens;
6. teatro degli Arcimboldi
Nell'area è presente anche una mensa interna alla Siemens. Per tale ragione questi lavoratori non sono inclusi tra quelli che possono andare nelle altre due mense.
Nelle simulazioni un cronotopo acceso è rappresentato in blu, o in celeste nel caso delle mense, mentre un cronotopo spento è colorato in nero. Il teatro degli Arcimboldi è sempre spento, perchè le
simulazioni sono fatte sempre nell'intervallo tipico delle attività diurne: dalle 7 alle 20. Gli uffici amministrativi hanno un orario d'apertura al pubblico, di cui si è tenuto conto. Questo
intervallo è all'interno dell'orario in cui gli edifici ospitanti sono cronotopi attivi. Questi sottocronotopi, detti topoi, non sono visibili graficamente.
Ogni cronotopo è caratterizzato da un orario d'apertura e chiusura che definisce la dinamica temporale del cronotopo stesso, e da una determinata capienza massima come riportato nella tabella 2.
| cronotopo | orario | capienza |
| facoltà umanistiche | 7:30-19:30 | 1500 |
| facoltà scientifiche | 7:30-19:30 | 1000 |
| CNR | 7:30-19:30 | 1000 |
| Siemens | 7:30-20:00 | 1000 |
|
scienze dei materiali |
7:30-19:30 | 1000 |
| uffici amministrativi | 8:00-19:00 | 1000 |
| mensa MU | 11:30-15:00 | 500 |
| mensa MS | 11:30-15:00 | 50 |
Tabella 2. Orario d'apertura e chiusura dei cronotopi e la loro capienza massima.
Frequenze e capacità dei mezzi di trasporto pubblico
Le fermate dei mezzi di trasporto pubblico sempre nella figura 8 sono rappresentate in verde chiaro, inclusa la stazione ferroviaria Greco Pirelli in basso. Sono stati forniti in input tutti gli orari delle linee di autobus che transitano nell'area e dei treni che fermano nella stazione Greco Pirelli. Le fermate degli autobus e la stazione sono considerate come sorgenti d’utenti e come pozzi. In queste aree sono creati mobber che contribuiscono alla mobilità pedonale totale osservabile nell'area, e al tempo stesso, assorbono i mobber che si allontanano. Sono stati riportati gli orari in un verso di percorrenza e nell'altro per tutte le fermate, questo perché gli orari possono essere sfasati e bisogna tener conto di tale differenza. Nella stazione dei treni sono presenti solo gli arrivi. Il numero di mobber generati nelle fermate dei mezzi pubblici e nei parcheggi rispecchia le percentuali con cui gli utenti possono arrivare nell'area di Milano Bicocca come si presentano nella tabella 3.
| mezzi di trasporti | % |
|---|---|
| auto | 15-20 |
| treno | 60 |
| autobus | 13-8 |
| bicicletta | 6 |
| a piedi | 6 |
Tabella 3. Mezzi di trasporto usati per arrivare nell'area di Milano Bicocca.
Protocollo di rilevamento dati
In due periodi distinti abbiamo registrato dati di mobilità con modalità sperimentali diverse. In entrambi i casi abbiamo registrato i tracciati pedonali effettuati nell'area presa in esame
mediante GPS per poter fare un confronto tracciato per tracciato tra quello registrato e quello simulato.
La prima volta abbiamo ipotizzato che gli osservatori coincidessero con gli osservati. A 10 studenti sono stati dati 10 GPS, ognuno col compito di registrare tutti i percorsi effettuati in tre
giorni successivi. I dati sono stati presi su un periodo temporale molto ampio, da metà febbraio agli inizi di luglio 2002.
In questo modo si pensava di poter monitorare la mobilità pedonale interna all'area e quella presente nei nodi di interscambio con gli altri mezzi di trasporto (auto, moto, treni). Purtroppo in
questo caso l'intervallo temporale di registrazione non è stato costante. Questo perché, spesso, soprattutto in treno o in moto ad alte velocità, si può perdere la ricezione del segnale. Inoltre le
velocità presentavano una forte variabilità. Anche questo è un errore legato alla ricezione del segnale. Il range delle velocità è ampio a causa dei diversi mezzi di trasporto: dalle velocità dei
treni a quelle dei pedoni. Tra tutti i 37 segnali registrati ne sono stati selezionati pochissimi da utilizzare in un confronto con i tracciati simulati. Dapprima sono stati scartati i tracciati
con pochi punti e ne sono rimasti 34. Tra questi alcuni presentano velocità troppo elevate, il che esclude che il moto sia pedonale. Dei 23 tracciati con alcuni tratti pedonali ne sono stati
selezionati 9 utili per fare un confronto puntuale. Come si può capire questi sono pochi per fare una statistica dei tracciati.
Allora abbiamo deciso di rimisurare i dati con altre modalità più funzionali ad un confronto tra tracciati simulati e quelli misurati.
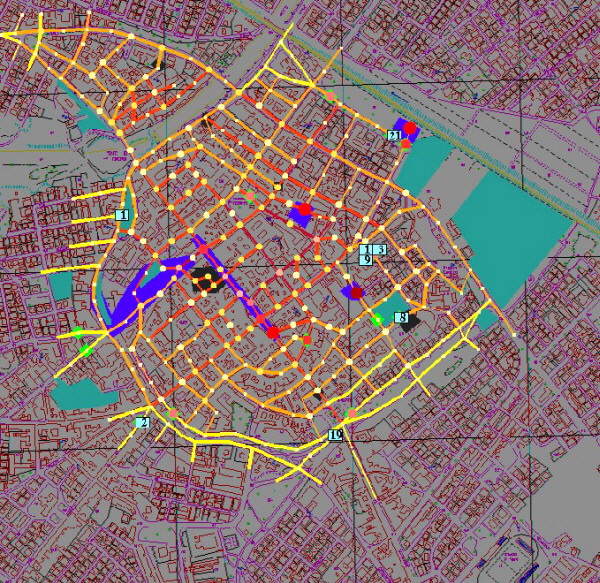
I tracciati registrati si presentano come si vede nella figura 9.
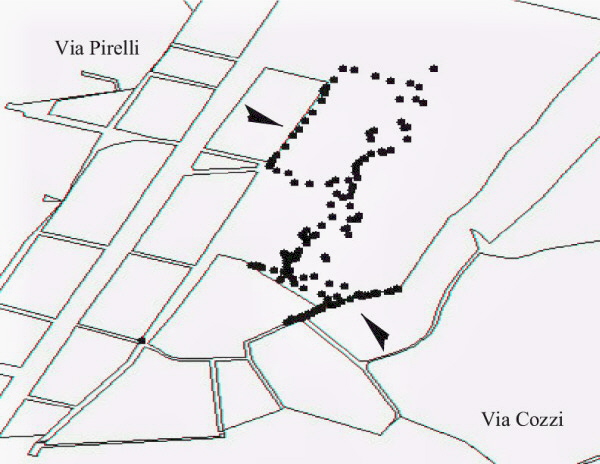
Durante il secondo periodo di rilevamento dei dati abbiamo scelto di introdurre una distinzione tra osservatore e osservato: gli osservatori (13 studenti), identificati da una lettera dell'alfabeto
(A, B, C, D, E, F, G, H, I, L, M, N, O) sono stati muniti di GPS (modello geko201). L'osservatore, a questo punto, ha seguito i percorsi (pedonali) di diverse persone scelte a caso entro alcune
fasce orarie definite a priori nei diversi momenti della giornata. Inoltre questa volta l’intervallo di rilevamento dati è stato definito costante nelle misure effettuate.
Durante il tragitto, ad ogni osservato, è stato fatto compilare un questionario costruito per rilevare alcune caratteristiche sociologiche degli attori della mobilità osservabile nell'area, da
utilizzare nell'analisi dei flussi. Abbiamo utilizzato in un secondo momento questi dati per comprendere gli spostamenti delle diverse categorie sociali, per distinguere, per esempio, gli
spostamenti degli studenti da quelli dei lavoratori o dei residenti, gli spostamenti di chi fa la pausa pranzo da chi non la fa, gli spostamenti degli utenti di mezzi pubblici per arrivare
nell'area da quelli che usano i propri mezzi. Gli osservati erano liberi di muoversi entro i limiti dell'area. Usciti fuori, gli osservatori potevano considerare i percorsi degli osservati
conclusi. Erano concesse tutte le piccole soste, purché inferiori ai 15 minuti. Questo perché in un intervallo di tempo così lungo si riesce ad attraversare da parte a parte tutta l'area muovendosi
con un passo normale, cosa che avrebbe causato errori di interpretazione.
Durante la seconda campagna sono stati registrati solo tracciati pedonali. Purtroppo, in questo secondo caso, anche se la procedura di rilevamento si è rivelata buona.
I dati presi in tre giorni distinti sono troppo pochi per rintracciare eventuali differenze settimanali o anche stagionali [36]. I giorni
scelti sono: il 10.12.2004, il 13.12.2004 e il 14.12.2004. In ogni giorno si sono scelte tre fasce orarie: dalle 9 alle 10, la mattina (MA), dalle 12 alle 14, a mezzogiorno (MG), dalle 15 alle 17
(PO), nel pomeriggio, orario serale. L'intervallo temporale minimo, che intercorre tra un segnale e il successivo, in questo caso è costante ed è pari a 31 secondi (*).
Sono stati registrati 2.070 punti etichettati al variare della bontà del segnale in questo modo: A per ottimo, B per sufficiente e C per pessimo. Sono stati registrati complessivamente 155
tracciati.
Analisi dei dati
Abbiamo svolto una prima analisi dei punti registrati per togliere tutti i dati non affidabili seguendo tre criteri. Nel primo caso abbiamo eliminato i tracciati con una pessima affidabilità del
segnale. Nel secondo caso abbiamo eliminato i tracciati in cui le velocità medie utilizzate sono nelle code della distribuzione delle velocità (strumento non usato bene). Nell'ultimo caso, abbiamo
eliminato i tracciati con meno di 8 punti. Abbiamo scelto questo numero minimo di punti per poter considerare un percorso come una traiettoria per due motivi principali: il numero medio di punti
per traiettoria è di 13 e 8 punti sono percorribili in poco più di 4 minuti. Nel primo caso, poiché il numero totale di punti registrati è di 2.070, e possono essere suddivisi in 155 traiettorie,
si ha che il numero medio di punti per traiettoria è di almeno 13 e 8 punti coprono il 60% di una traiettoria media.
Nel secondo caso, poiché l'intervallo temporale che intercorre tra un segnale e il successivo è di 31 s, allora 8 punti si possono percorrere in poco più di 4 minuti, un tale intervallo corrisponde
a circa il 25% dell'intervallo di tempo massimo necessario per attraversare tutta l'area.
L'ultimo criterio racchiude i primi due. I tracciati con un numero di punti inferiore ad 8, in genere sono registrati con una pessima ricezione e con velocità improbabili per un moto pedonale come
per esempio circa 2.28 m/s (8.2 km/h). Abbiamo fatto l'analisi dei flussi osservati usando questo criterio selezionando dai 155 tracciati registrati, 136 che a loro volta sono stati utilizzati per
confrontare tra i flussi misurati con quelli simulati dal modello Mileto/Manhattan.
Rigettando traiettorie con meno di 8 punti, abbiamo eliminato 29 traiettorie su 155, scegliendo in questo modo un protocollo di misura con un'incertezza compresa tra il 20% e il 30%.
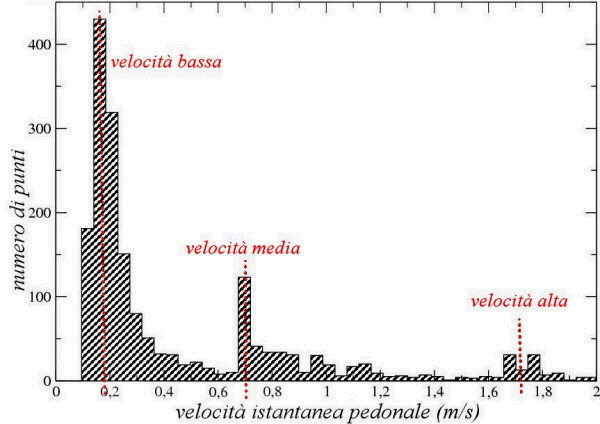
Ora possiamo passare all’analisi della distribuzione delle velocità che si possono ottenere dai dati registrati. In questo modo si vuole confrontare la velocità media registrata dei pedoni reali con la velocità usata dai mobber del modello, scelta pari a 1 m/s. Dall’analisi si ottiene che la maggior parte dei pedoni reali si muove ad una velocità molto bassa, di circa 0.2 m/s, quella tipica del flaneur, gli altri vanno ad un passo ragionevole, che è di circa 0.7 m/s, e solo pochi hanno un passo sostenuto, oltre 1.6 m/s (figura 10), allorché si è calibrato il moto introducendo attrito sotto forma di pause random durante il percorso dei mobbers.
Il numero di tracciati (NT) è espresso in funzione del numero di punti registrati (NP) per ogni tracciato e la lunghezza dell'intervallo temporale di registrazione* (tabella 4)**.
Il numero di tracciati registrati (NT) è riportato in funzione del giorno di registrazione (tabella 5) e delle fasce orarie di registrazione (tabella 6). Nelle stesse tabelle sono riportate i punti registrati (NPR), quelli selezionati (NPS) e l'errore percentuale (ER) del numero di punti selezionati su quelli registrati. I tracciati sono 136, i punti registrati 2070 e quelli selezionati 1491. Confrontando i punti selezionati con quelli registrati osserviamo che restiamo entro l'errore inizialmente stimato di almeno un 20%. Un tale errore cresce per i dati registrati il 10.12.2004, probabilmente perché è stato fatto un errore sistematico durante le registrazioni. Tale errore è più manifesto nei tracciati registrati il pomeriggio, mentre è nascosto nei tracciati del mattino e del mezzogiorno (tabella 6).
| NT | giorno | NPR | NPS | ER % |
| 48 | 10.12.05 | 852 | 428 | 50 |
| 43 | 13.12.05 | 553 | 501 | 10 |
| 45 | 14.12.05 | 665 | 562 | 15 |
Tabella 5. Il numero di tracciati (NT) in funzione del giorno,con il numero di punti registrati (NPR), il numero di punti selezionati (NPS) e l'errore percentuale (ER).
| NT | fascia oraria |
NPR |
NPS | ER % |
| 46 |
9:00-10:00 |
574 |
468 |
18 |
| 45 |
11:00-14:00 |
854 | 595 | 30 |
|
45 |
15:00-17:00 |
642 | 428 | 33 |
Tabella 6. Il numero di tracciati (NT) in funzione della fascia oraria di rilevamento, con il numero di punti registrati (NPR), il numero di punti selezionati (NPS) e l'errore percentuale (ER).
Abbiamo scelto di suddividere l'area di Milano Bicocca in un reticolo di 125 per 125 rettangoli considerando gli estremi geografici: la latitudine massima è latmax=45°52’74’’, quella minima
latmin=45°50’51’’, la longitudine massima è lonmax=9°22’18’’, quella minima lonmin=9°20’23’’.
I GPS usati misurano fino al centesimo di secondo e permettono di avere dati con un errore spaziale di circa 15 m. Un reticolo di 125 per 125 rettangoli permette di suddividere tutta l'area con
rettangoli di lato 20 m per 17 m (*), in questo modo l'errore dello strumento è dentro un rettangolo del reticolo e dentro uno di questi rettangoli del reticolo può esserci al più un solo
punto.
In questo modo abbiamo messo in evidenza i percorsi privilegiati nell'area in funzione dei giorni di misura e delle diverse fasce orarie in cui sono avvenute le misure.
I risultati dell'analisi dei flussi nei diversi giorni settimanali permettono di fare un'osservazione del tutto qualitativa, non si può fare una statistica, perché sono disponibili i dati di soli
tre giorni. Il venerdì pomeriggio (10.12.05) l'area universitaria è poco frequentata, così come il lunedì mattina (13.12.05). Il giorno in cui si è a regime con massimi di flusso la mattina e il
pomeriggio è il martedì (14.12.05).
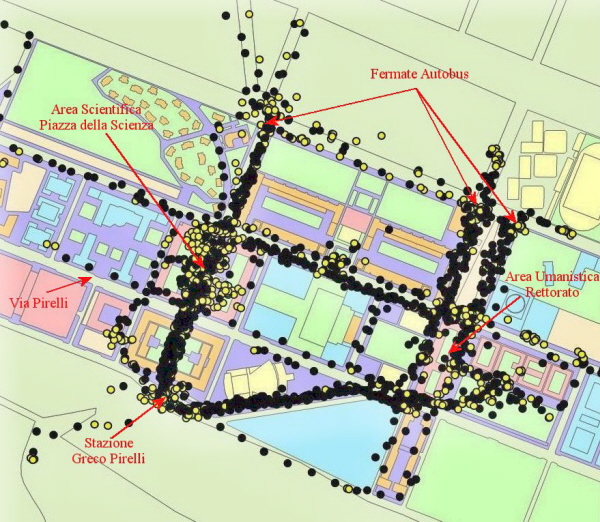
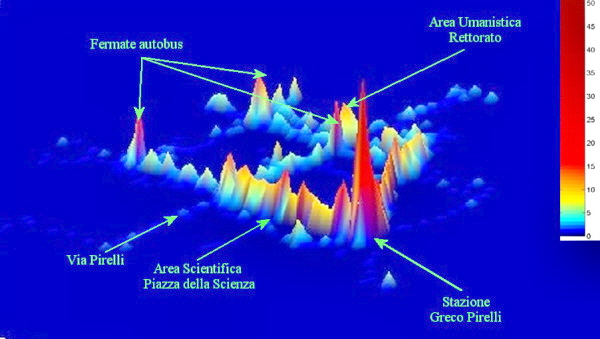
Le traiettorie registrate nell'area di Milano Bicocca durante tutti e tre i giorni (figura 11) in tre dimensioni (figura 12).
Simulazioni
Dopo aver definito le caratteristiche dei cronotopi e delle sorgenti dell'area Milano Bicocca, passiamo a considerare le caratteristiche dei mobber. Per ogni mobber abbiamo costruito un'ipotetica agenda con un certo numero d'attività da svolgere durante tutto l'intervallo di permanenza del mobber nell'area, in funzione delle diverse attività che si possono svolgere nei diversi cronotopi. La distribuzione delle attività presenti nelle agende dei mobber segue la tabella 7 sottostante:
| % | Attività |
| 40 | 2 |
| 10 | 3 |
| 50 | 4 |
Tabella 7. Percentuali (%) con cui sono creatii mobber aventi un certo numero d’attività in agenda.
Ogni mobber può essere attratto da un certo tipo di cronotopo e non da altri secondo una propria maschera interna, definita seguendo le caratteristiche sociologiche e che costituisce una sorta di “patrimonio genetico” del mobber. Per esempio i lavoratori della Siemens, che arrivano in azienda, durante l'orario del pasto vanno nella loro mensa interna e per questo non usciranno dal loro cronotopo principale dove sono arrivati al mattino per recarsi nelle altre mense presenti nell'area come possono fare gli altri. Per esempio gli studenti, i ricercatori e i professori possono andare nella mensa del CNR (MS) e in quella generale posta nell'edificio U7 (MU). I mobber, una volta creati, assumono comportamenti vincolati dal numero d'attività in agenda (numero di cronotopi da visitare) e dal tempo di permanenza nei cronotopi visitati (tabella 8).
| agenda svolta da un mobber |
% |
tempi di permanenza |
|
CNR – casa |
4 | 4h (10%) - 6h (20%) - 8h (70%) |
|
SIEMENS – casa |
10 |
4h (10%) - 6h (20%) - 8h (70%) |
|
facoltà scientifiche (FS) - casa |
19 | 5h (40%) - 9h (60%) |
|
facoltà umanistiche (FU) - casa |
47 | 4h (60%) - 9h (40%) |
| uffici – casa | 20 | 1h (20%) - 5h (20%) - 7h(60%) |
| FU - mensa(M2) - casa | 67 | 3h (FU) - 1h (M2) |
| FS - mensa(M1) - casa | 33 | 4h (FS) - 1h (M1) |
| FU - mensa(M2) – FU - casa | 75 | 3h (FU) - 1h (M2) - 4h (FU) |
|
FS - mensa(M1) – FS - casa |
25 | 4h (FS) - 1h (M1) - 4h (FS) |
Tabella 8. L'agenda di un mobber espressa in funzione dei tempi di permanenza nei cronotopi visitati.
Risultati
Flussi dalle 9:00 e le 10:00
La stazione e le fermate degli autobus sono le sorgenti principali, rispetto ai parcheggi, della mobilità osservabile nell'area, ossia, coloro che si recano all'Università Milano Bicocca lo fanno
con mezzi di trasporto pubblico piuttosto che con mezzi privati. Inoltre la popolazione degli studenti è sicuramente quella prevalente sulle altre.
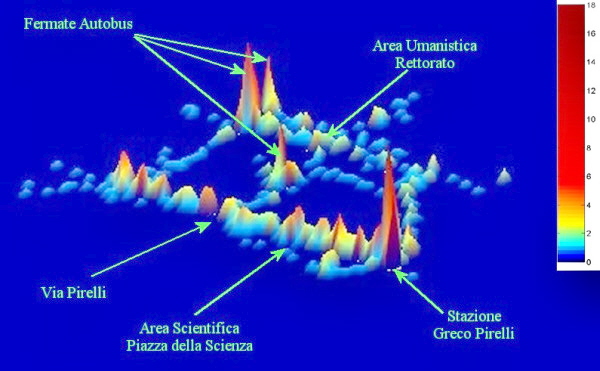
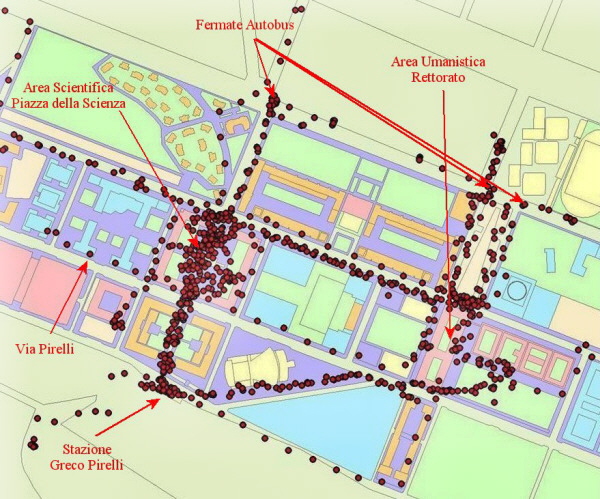
Confrontando i flussi registrati (figura 13) e quelli simulati (figura 14) nella fascia oraria tra le 9:00 e le 10:00 abbiamo riscontrato una netta correlazione tra i picchi di massimo delle due
fermate dell'autobus 727, in alto al centro nella figura 13, e quello degli arrivi in stazione, in basso a destra nella figura 13 e i flussi riprodotti nella figura 14. Il codice dei colori è
simile nelle due figure: dal giallo, minimo di densità-flusso, al rosso, massimo di densità-flusso. In entrambe le figure si possono osservare gli spostamenti diretti nelle facoltà scientifiche.
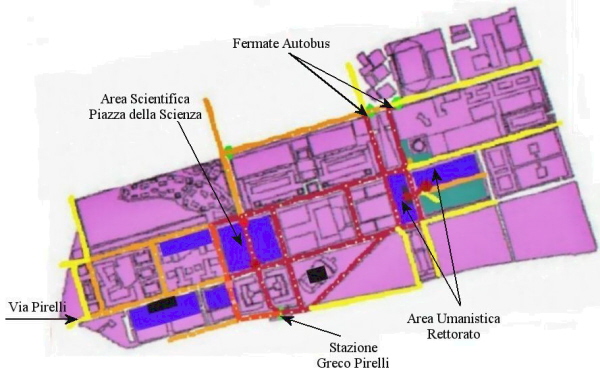
Le figure successive (figura 15 e 16) sono state ottenute selezionando alcuni tracciati sui flussi di mobilità diretta dalla stazione ferroviaria di Greco Pirelli e dalle fermate degli autobus alle facoltà scientifiche e umanistiche.


Flussi dalle 12:00 e le 14:00
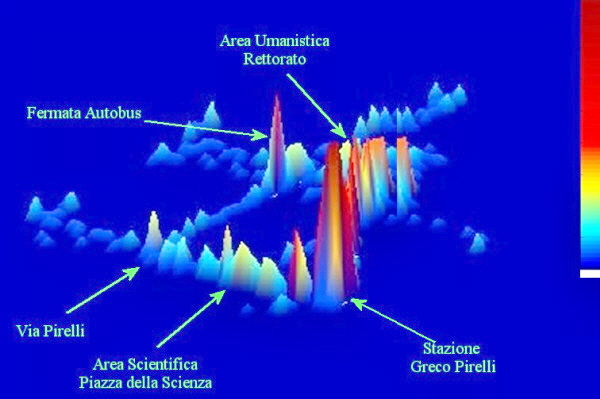
Confrontiamo i flussi registrati (figura 17) con quelli simulati (figura 18) nella fascia oraria tra le 12:00 e le 14:00. Spiccano gli arrivi in stazione e un’elevata mobilità che lega stazione e piazza della Scienza (figura 17), ossia le facoltà scientifiche. Questo si può interpretare come un arrivo in stazione degli studenti che si recano nelle facoltà umanistiche e come un flusso di studenti delle facoltà scientifiche che si recano a casa. Il picco di presenze in mensa MU (figura 17) è ben visibile. Tale picco corrisponde, nelle simulazioni, all'area colorata al centro del cronotopo (figura 18).


I tracciati registrati nella fascia oraria della pausa pranzo sono riportati nella figura 19. Come si vede la mensa MU è un cronotopo con una certa forza attrattiva, mentre nella Piazza della Scienza si osserva la presenza di un gran numero di pedoni in sosta perché mangiano un panino al volo, oppure si dirigono verso la stazione per ritornare a casa dopo le lezioni della mattina.
Flussi dalle 15:00 e le 17:00
Confrontiamo i flussi registrati (figura 20) con quelli simulati (figura 21) nella fascia oraria del pomeriggio dalle 15:00 alle 17:00.
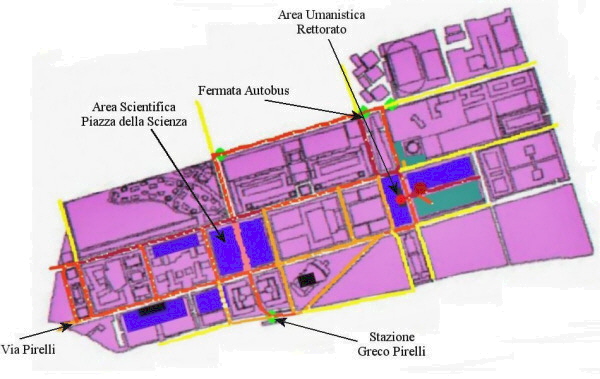
Nel pomeriggio, il flusso, che va dalla stazione alle facoltà umanistiche, è maggiore di quello che va dalla stazione alle facoltà scientifiche (figura 20). Nelle seguenti figure sono riportati gli
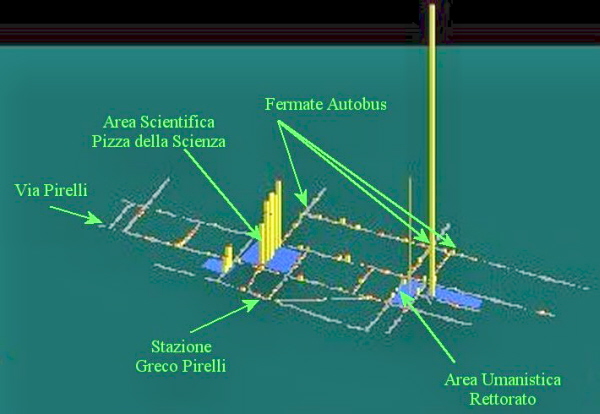
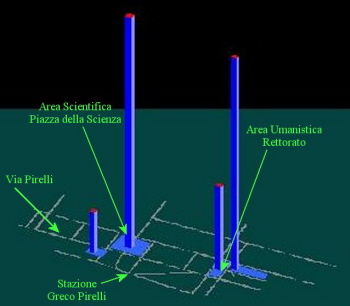
istogrammi che monitorizzano la mobilità dei pedoni lungo le strade (figura 22) nei nodi del reticolo e le presenze nei diversi cronotopi accesi (figura 23).
Entrambe le figure sono state ottenute facendo una simulazione con Mobilis e scegliendo la fascia oraria del mattino. Come si vede il cronotopo delle facoltà scientifiche è molto attivo, ma lo è
anche quello del settore amministrativo, visto che gli uffici aprono al pubblico tra le 9:00 e le 11:00.
Il cronotopo delle facoltà scientifiche è più affollato, in genere, di quello delle facoltà umanistiche. Il divario, come si è potuto vedere, si accentua nella fascia oraria della mattina.
Conclusioni
La procedura di simulazione descritta ha fornito risultati sufficientemente congruenti, nonostante si sia confrontato un numero esiguo di dati (155 tracciati) con un numero di pedoni simulati in
Mobilis, superiore di un fattore 100 rispetto a quello registrato tramite GPS. Possiamo quindi affermare che, per quanto attiene la mobilità nell'area di Milano Bicocca, il comportamento dei pedoni
reali (individui umani) è abbastanza ben riprodotto dal comportamento dei pedoni virtuali (mobber).
Questo risultato ci ha spinto a percorrere altre strade per migliorare da una parte l’implementazione teorica del modello e dall’altra trovare le congruenze tra quello che il modello riproduce e il
fenomeno reale che si vuole riprodurre.
Durante il Carenevale di Venezia del 2006 esattamente dal 15.02.2006 al 28.02.2006 abbiamo fatto una campagna cospicua di misure. Si sono registrati molti percorsi su tutta l’area di Venezia dando
particolare risalto ai flussi durante alcuni eventi significativi del carnevale (come il carnevale dei piccoli in Campo San Polo, oppure la notte del tango Argentino, oppure la sfilata di apertura
e la chiusura del carnevale stesso). L’obiettivo in questo caso sarà la riproduzione della mobilità su tutta l’area cittadina (non ristretta a quella di un singolo quartiere, come nel caso di
Milano Bicocca) che coinvolge centinaia di migliaia di persone e non poche migliaia (come fu per Rimini).
Ovvero, fino ad ora abbiamo operato in condizioni di bassa densità (qualche migliaio di individui).
Se si vuole condizioni favorevoli. A Venezia sperimentiamo il modello in situazioni di affollamento e con centinaia di migliaia di componenti elementari. Cioè condizioni assai più difficili.
Per far questo sono serviti 10 gg. di rilevamenti ed un apparato sperimentale più complesso, costituito da diversi strumenti: dalle telecamere che registrano la dinamica dell’intera folla o dei
flussi al contorno, ai GPS che monitorizzano il singolo individuo in quella che si presenta come una dinamica collettiva turbolenta legata ai ritmi delle attività circostanti, a quelli biologici ed
anche a quelli della logistica.
Sitografia di riferimento:
www.physycom.unibo.it
www.fisicadellacitta.it
www.casa.ucl.ac.uk
www.trafficforum.org
www.intelligentspace.com
Bibliografia di riferimento
J. Barros, F. Sobreira, City of slums: self-organization across scales, CASA, 2002: http://www.casa.ucl.ac.uk/working_papers/paper55.pdf
M. Batty, Modelling cities as dynamic systems, «Nature», 231 (1971), p. 425.
M. Batty, The emergence of cities: complexity and urban dynamics, CASA, 2003: http://www.casa.ucl.ac.uk/working\_papers/paper64.pdf.
M. Batty, Cities and Complexity, Cambridge (MA), MIT Press, 2005.
M. Batty M., J. DeSyllas, E. Duxbury, The discrete dynamics of small-scale spatial events: agent based models of mobility in carnivals and street parades, CASA, 2002: http://www.casa.ucl.ac.uk/working_papers/paper56.pdf.
M. Batty, P.M. Torrens, Modelling complexity: the limits to prediction, CASA, 2001: http://www.casa.ucl.ac.uk/paper36.pdf.
M. Batty, Y. Xie, Possible urban automata, Venezia, DAEST, 1996.
A. Bazzani, M. Capriotti, B. Giorgini, G. Servizi, G. Turchetti, G. Melchiorre, S. Luccardi, M. Zaoli, Un modello per la mobilità asistematica nel Centro Storico di Rimini, «T&T» 4 (2003), 141-149.
A. Bazzani, B. Giorgini, G. Servizi, G. Turchetti, Modello cronotopico di mobilità, Rapporto MURST Ricerca di Rilevante Interesse Nazionale “Tempi urbani”, 1999.
A. Bazzani, B. Giorgini, G. Servizi, G. Turchetti, Mobilis in Mobile: a probabilistic and chronotopic model of mobility in urban spaces, «Biology Forum», 3/94 (2001).
A. Bazzani, B. Giorgini, G. Servizi, G. Turchetti, A chronotopic model of mobility in urban spaces, «Physica A», 325 (2003).
E. Besussi, A. Cecchini (eds.), Artificial world and urban studies, Venezia, DAEST, 1996
S. Bonfiglioli, Che cos'è un cronotopo, in S. Bonfiglioli, M. Mareggi (eds.), Il tempo e la città tra natura e storia. Atlante dei progetti sui tempi della città, Roma, Urbanistica Quaderni INU, 1997.
E. Cascetta, G.E. Cantarella, Modelling dynamics in transportation networks: state of the art and future developments, «Journal of Simulation Practice and Theory», 1 (1993).
A. Cecchini, Are urban model useful?, Venezia, DAEST, 1996.
M. Ciccotti, B. Giorgini, The emergence of complexity in a common scotch roller, in L. Boi (ed.), Symétries, brisures de symétries et complexité en mathématiques, physique et biologie, Bern, Peter Lang, 2006.
B. Giorgini, Il tempo del caos, in S. Bonfiglioli, M. Mareggi (eds.), Il tempo e la città tra natura e storia. Atlante dei progetti sui tempi della città, Roma, Urbanistica Quaderni INU, 1997.
B. Giorgini, Philosophie naturelle de la causalité et du hasard dans un modèle de mobilité urbaine, in corso di pubblicazione, in S. Franceschelli, M. Paty, T. Roque (eds.), Éléments pour une èpistémologie des systèmes dynamiques, Hermann.
B. Giorgini, G. Turchetti, From Newton-Boltzmann paradigms to complexity: a bridge to bio-systems, in The Science of Complexity: Chimera or Reality, Bologna, Esculapio, 2006.
D. Helbing, Traffic and related self-driven many-particle systems, «Reviews of Modern Physics», 73 (2001).
B. Hiller, A theory of the city as object, 3rd Syntax Symposium, Atlanta, 2001.
B. Hutchinson, M. Batty (eds.), Advances in urban systems modelling, Amsterdam, North Holland, 1986.
S. Kauffman, A casa nell'universo, le leggi del caos e della complessità (1995), Roma, Editori Riuniti, 2001.
D.B. Lee, Requiem for large scale models, «Journal of American Institute of Planners», 39 (1973).
G. Martinotti, Metropoli: la nuova morfologia sociale della città, Bologna, il Mulino, 1997.
G. Melchiorre, Misure ed esperimenti nella fisica della città, Tesi di dottorato, 2006.
G. Melchiorre, A. Bazzani, M. Capriotti, B. Giorgini, S. Rambaldi, G. Servizi, G. Turchetti, Relazioni temporali tra flussi di mobilità metropolitana nell'area di Châtelet-Les Halles, T&T, 3 (2004).
G. Melchiorre, A. Bazzani, M. Capriotti, B. Giorgini, G. Servizi, G. Turchetti, Ritmi temporali nell'area di Châtelet-Les Halles, in corso di pubblicazione nella sezione Progetti Urbani della collana “Città Tempo Architettura”.
G. Parisi G., La nuova fisica statistica e la biologia, Bologna, il Mulino, 1992.
H. Poincaré, Geometria e caso a cura di C. Bartocci, Torino, Bollati Boringhieri, 1995.
Proceedings del convegno Forum Internazionale sulla mobilità sostenibile nelle aree metropolitane, Verona 23-24 ottobre 2003.
R. Rosini [et al.], Campagna di rilevazione sui comportamenti e sulle preferenze dei cittadini in materia di mobilità, Regione Emilia-Romagna, 2003.
F. Schweitzer, Self-Organization of complex structures: from individual to collective dynamics, London, Gordon and Breach, 1997.
M.C. Taylor, Il momento della complessità (2001), Codice Edizioni, 2005.
G. Turchetti, Theory and computation for non linear dynamical models, REH-SEIS (CNRS et Université Paris 7 “Denis Diderot”) e Università degli studi di Bologna - Dip. di Fisica, 1999.
M.V. Volkenstein, Physical approach to biological evolution, Berlin, Springer, 1994.
Note
[1] M. Batty, Cities and Complexity, Cambridge Mass., MIT, 2005.
[2] J. Barros, F. Sobreira, City of slums: self-organization across scales, CASA, 2002: disponibile al sito
http://www.casa.
ucl.ac.uk/working
_papers/paper55.pdf.
[3] Cfr. Proceedings del convegno Forum Internazionale sulla mobilità sostenibile nelle aree metropolitane, Verona 23-24 ottobre 2003.
[4] B. Giorgini, Il tempo del caos, in S. Bonfiglioli, M. Mareggi (eds.), Il tempo e la città tra natura e storia, atlante dei progetti sui tempi della città, Roma, Urbanistica Quaderni INU, 1997, 325.
[5] M.B. Ciccotti, B. Giorgini, The emergence of complexity in a common scotch roller, in L. Boi (ed.), Symétries, brisures de symétries et complexité en mathématiques,physique et biologie, Bern, Peter Lang, 2006, 187-216.
[6] Cfr. S. Kauffman, A casa nell'universo, le leggi del caos e della complessità, Roma, Editori Riuniti, 2001 (ed.or.: Oxford University Press, 1995).
[7] Cfr. G. Parisi, La nuova fisica statistica e la biologia (Sistemi Intelligenti, 2), Bologna, il Mulino, 1992.
[8] Cfr. B. Giorgini, G. Turchetti, From Newton-Boltzmann paradigms to complexity: a bridge to bio-systems, The Science of Complexity: Chimera or Reality (Milan Research for Industrial and Applied Mathematics), Bologna, Esculapio, 2006, 18-31.
[9] B. Giorgini, Philosophie naturelle de la causalité et du hasard dans un modèle de mobilité urbaine, in corso di stampa in S. Franceschelli, M. Paty, T. Roque (eds.), Éléments pour une épistémologie des systèmes dynamiques, Hermann.
[10] M.V. Volkenstein, Physical approach to biological evolution (con il contributo di M. Eigen), Berlin, Springer, 1994.
[11] D.B. Lee, Requiem for large scale models, «Journal of American Institute of Planners», 39 (1973), 163.
[12] M. Batty, Modelling cities as dynamic systems, «Nature», 231 (1971), 425.
[13] B. Hutchinson, M. Batty (eds.), Advances in urban systems modelling, Amsterdam, North Holland, 1986.
[14] B. Hiller, A theory of the city as object, 3rd Syntax Symposium, Atlanta 2001.
[15] H. Poincaré, Geometria e caso a cura di C. Bartocci, Torino, Bollati Boringhieri, 1995.
[16] M. Batty M., P.M. Torrens, Modelling complexity: the limits to prediction, CASA, 2001, disponibile al sito
http://www.casa.
ucl.ac.uk/
paper36.pdf.
[17] M. Batty, Y. Xie, Possible urban automata, Venezia, DAEST, 1996; E. Besussi, A. Cecchini (eds), Artificial world and urban studies, Venezia, DAEST, 1996.
[18] M.C. Taylor, Il momento della complessità, Codice Edizioni, 2005 (si veda anche The Moment of Complexity Emergine Network Culture, Chicago, University of Chicago Press, 2001).
[19] M. Batty, J. DeSyllas, E. Duxbury, The discrete dynamics of small-scale spatial events: agent based models of mobility in carnivals and
street parades, CASA, 2002, disponibile al sito
http://www.casa.
ucl.ac.uk/
working_papers/
paper56.pdf ;
M. Batty, The emergence of cities: complexity and urban dynamics, CASA, 2003, disponibile al sito
http://www.casa.
ucl.ac.uk/
working\_papers
/paper64.pdf ; F. Schweitzer, Self-Organization of complex structures: from individual to collective dynamics, London, Gordon & Breach, 1997, 19-24.
[20] G. Turchetti, Theory and computation for non linear dynamical models, REH-SEIS (CNRS et Université Paris 7, Denis Diderot) & Università di Bologna - Dip. di Fisica, Paris 1999.
[21] G. Martinotti, Metropoli: la nuova morfologia sociale della città, Bologna, il Mulino, 1997.
[22] J. Barros, F. Sobreira, City of slums cit.
[23] A. Cecchini, E. Besussi, Artificial worlds and urban studies, Venezia, DAEST 1996; A. Cecchini, Are urban model useful?, Venezia, DAEST, 1996, 7-16.
[24] E. Cascetta, G.E. Cantarella, Modelling dynamics in transportation networks: state of the art and future developments, «Journal of Simulation Practice and Theory», 1 (1993), 65-69.
[25] D. Helbing, Traffic and related self-driven many-particle systems, «Reviews of Modern Physics», 73 (2001), 1067-1141.
[26] R. Rosini et al., Campagna di rilevazione sui comportamenti e sulle preferenze dei cittadini in materia di mobilità, Regione Emilia-Romagna, 2003.
[27] G. Martinotti, Metropoli: la nuova morfologia sociale della città, Bologna, il Mulino, 1997.
[28] B. Giorgini, Philosophie naturelle de la causalité et du hasard dans un modèle de mobilité urbaine, in corso di pubblicazione in S. Franceschelli, M. Paty, T. Roque (eds.), Éléments pour une épistémologie des systèmes dynamiques, Hermann, 2006.
[29] D.B. Lee, Requiem for large scale models, «Journal of American Institute of Planners», 39 (1973), 163.
[30] M. Batty, Modelling cities as dynamic systems, «Nature», 231 (1971), 425.
[31] A. Bazzani, M. Capriotti, B. Giorgini, G. Servizi, G. Turchetti, G. Melchiorre, S. Luccardi, M. Zaoli, Un modello per la mobilità asistematica nel Centro Storico di Rimini, «T&T» 4 (2003), 141-49.
[32] G. Melchiorre, Misure ed esperimenti nella fisica della città, Tesi di dottorato, 2006.
[33]A. Bazzani, B. Giorgini, G. Servizi, G. Turchetti, Modello cronotopico di mobilità. Rapporto MURST Ricerca di Rilevante Interesse Nazionale “Tempi urbani”, 1999; A. Bazzani, B. Giorgini, G. Servizi, G. Turchetti, Mobilis in Mobile: a probabilistic and chronotopic model of mobility in urban spaces, «Biology Forum», 3/94 (2001), 499-509; A. Bazzani, B. Giorgini, G. Servizi, G. Turchetti, A chronotopic model of mobility in urban spaces, «Physica A», 325 (2003), 517-30.
[34] A. Bazzani [et al.], Un modello per la mobilità asistematica cit.
[35] G. Melchiorre, A. Bazzani, M. Capriotti, B. Giorgini, S. Rambaldi, G. Servizi, G. Turchetti, Relazioni temporali tra flussi di mobilità metropolitana nell'area di Châtelet-Les Halles, «T&T», 3 (2004), 99-106; G. Melchiorre, A. Bazzani, M. Capriotti, B. Giorgini, G. Servizi, G. Turchetti, Ritmi temporali nell'area di Châtelet-Les Halles, in corso di pubblicazione nella sezione Progetti Urbani della collana “Città Tempo Architettura”.
[36] Ivi.


 Creative Commons Attribution-NonCommercial-NoDerivatives 4.0
International License 2004- 2025
Creative Commons Attribution-NonCommercial-NoDerivatives 4.0
International License 2004- 2025
